Abstract
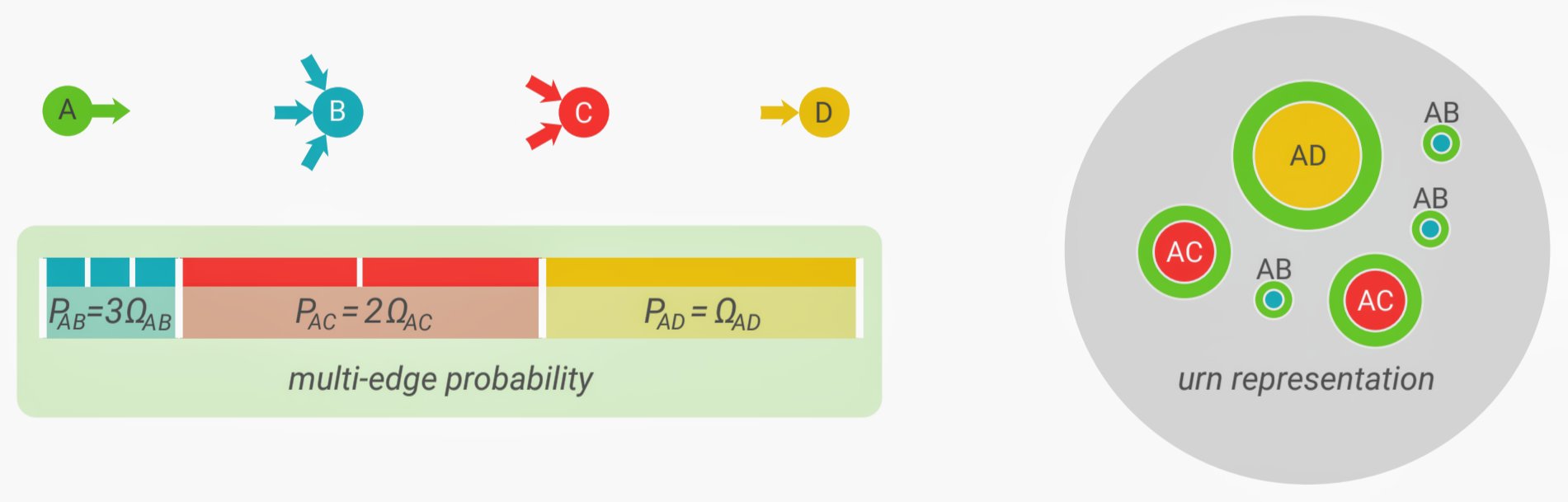
A fundamental issue of network data science is the ability to discern observed features that can be expected at random from those beyond such expectations. Configuration models play a crucial role there, allowing us to compare observations against degree-corrected null-models. Nonetheless, existing formulations have limited large-scale data analysis applications either because they require expensive Monte-Carlo simulations or lack the required flexibility to model real-world systems. With the generalized hypergeometric ensemble, we address both problems. To achieve this, we map the configuration model to an urn problem, where edges are represented as balls in an appropriately constructed urn. Doing so, we obtain the generalized hypergeometric ensemble of random graphs: a random graph model reproducing and extending the properties of standard configuration models, with the critical advantage of a closed-form probability distribution.