Abstract
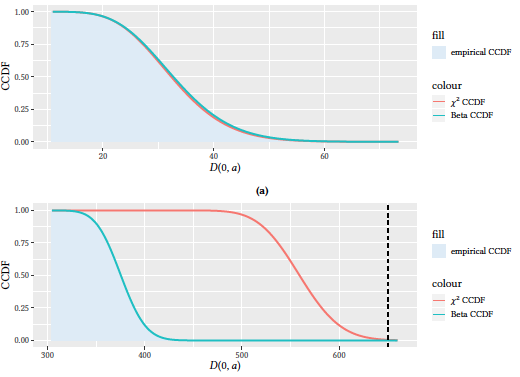
The complexity underlying real-world systems implies that standard statistical hypothesis testing methods may not be adequate for these peculiar applications. Specifically, we show that the likelihood-ratio test's null-distribution needs to be modified to accommodate the complexity found in multi-edge network data. When working with independent observations, the p-values of likelihood-ratio tests are approximated using a $χ^2$ distribution. However, such an approximation should not be used when dealing with multi-edge network data. This type of data is characterized by multiple correlations and competitions that make the standard approximation unsuitable. We provide a solution to the problem by providing a better approximation of the likelihood-ratio test null-distribution through a Beta distribution. Finally, we empirically show that even for a small multi-edge network, the standard $χ^2$ approximation provides erroneous results, while the proposed Beta approximation yields the correct p-value estimation.